аÄÃÅÁùºÏ²ÊÄÚÄ»ÐÅÏ¢

Korean mathematician Jineon Baek may have come up with a proof for a long-standing problem: What is the largest object that can fit around a corner of a certain size? 

Aptly described as the "moving sofa problem," this question was formally posed in 1966. In 1992, Joseph Gerver came up with a shape rather like an old-fashioned telephone handset as having the largest possible area, 2.2195 units if the hallway is one unit wide. Baek's proof, published as a , shows that Gerver's sofa is indeed the largest possible object that can fit round that corner. 

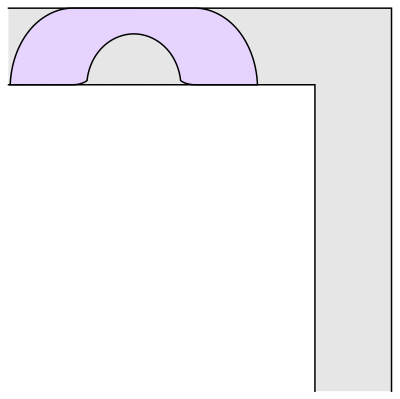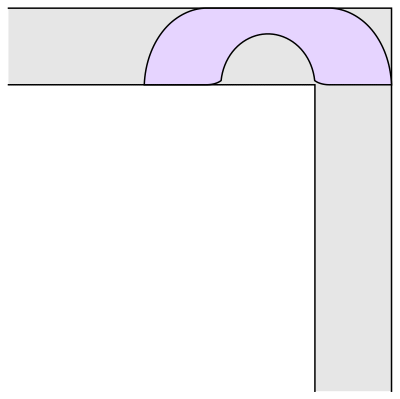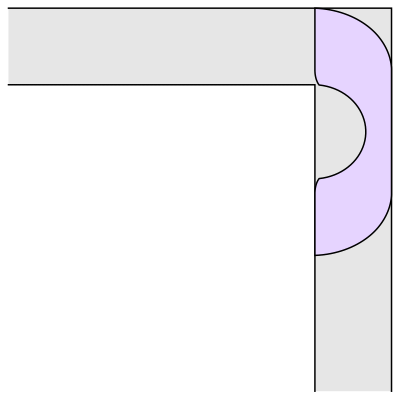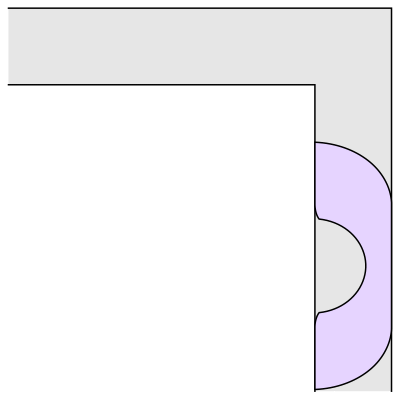
аÄÃÅÁùºÏ²ÊÄÚÄ»ÐÅÏ¢ Davis mathematician Dan Romik has worked on the and has a web page dedicated to it. His work is also featured in this . 

, Romik used 3-D printing to address a variation of the problem: What if there are two corners in opposite directions? Romik's solution proposes a dumbell-like shape with two wide sections connected by a pinched-in middle. 

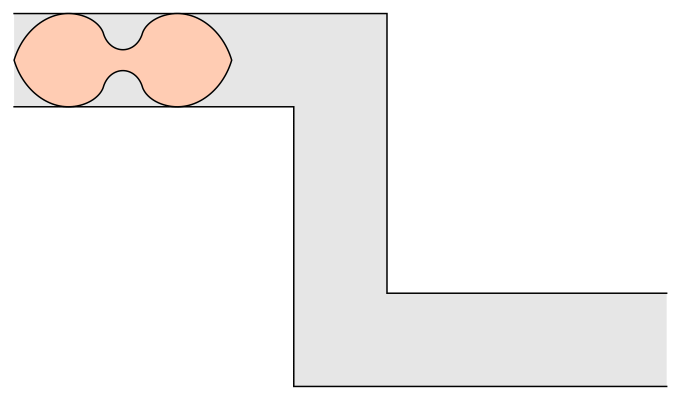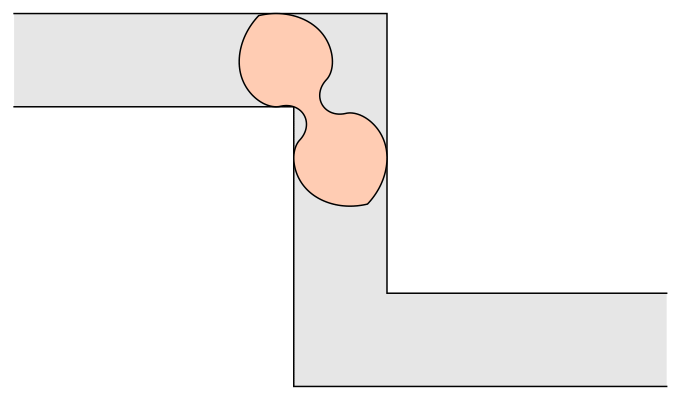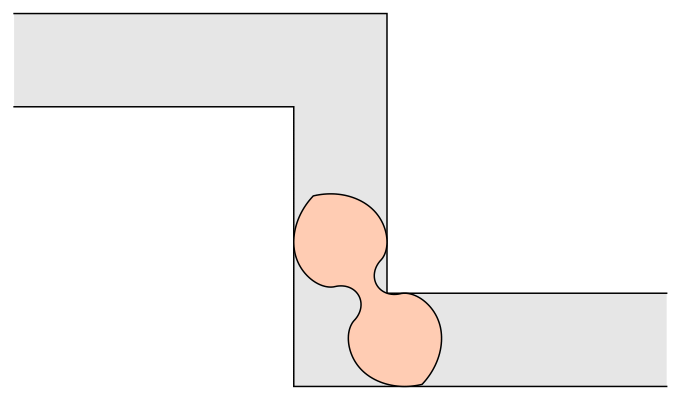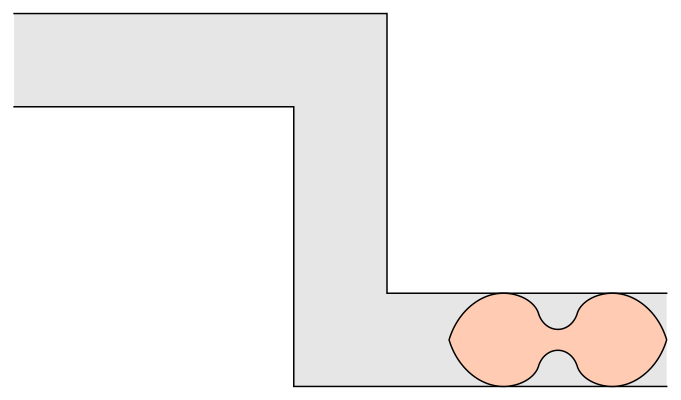
Apart from moving oddly-shaped furniture, what is the application of this? One example could be in understanding how fibers suspended in a fluid behave when they pass through a nozzle. Like most things in mathematics, ideas from the abstract have a way of showing up in the real world sooner or later.